


. تعريف المربع وخصائصه . الفرق بين المربع والمعين . حساب مساحة المربع . حساب محيط المربع . طريقة رسم المربع . أمثلة متنوعة حول المربع . المراجع تعريف
يُمكن تعريف المربع (بالإنجليزية: Square) على أنَّه عبارة عن شكل هندسي رُباعي الأضلاع، جميع أضلاعه مُتساوية في الطول، ومكوّن من أربعة زوايا داخلية قياس كل منها 90 درجة،[١] كما يُعرف المُربع على أنّه عِبارة عن حالة خَاصة من حالات المستطيل، إذ يتشابه مع المُستطيل بالأضلاع الأربعة المُستقيمة، وبالزوايا الداخليَّة القائمة ذات قياس 90 درجة، بالإضافة إلى أنَّ أقطاره تُنصِّف بعضها البعض، وكل ضلعين متقابلين فيه متوازيان ومتساويان، إلَّأ أنَّه يختلف عن المستطيل من ناحية أن جميع أضلاعه مُتساوية الطول، كما أن أقطاره متعامدة خلافاً للمستطيل،[٢] وبالإضافة إلى ما سبق يتميز المربع بالخصائص الآتية:[٣][٤]
لمزيد من المعلومات والأمثلة حول أقطار المربع يمكنك قراءة المقال الآتي: ما هو قطر المربع.
‘);
}
لمزيد من المعلومات والأمثلة حول ضلع المربع يمكنك قراءة المقال الآتي: ما هو قانون طول ضلع المربع.
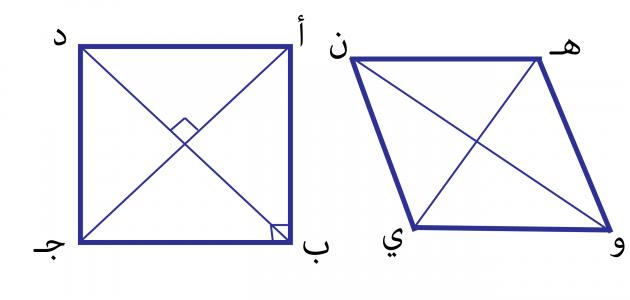
يعتبر كل من المعين والمربع عبارة عن أشكال رباعية، ويصنفان على أنهما حالات خاصة من متوازي الأضلاع؛ حيث يمتلك كل منها أربعة أضلاع، كل ضلعين متقابلين منها متوازيان، كما أن جميع أضلاعهم متساوية في الطول، وأقطارهم متعامدة على بعضها، إلا أن الاختلافات الرئيسية بين المربع والمعين هي: أن جميع زوايا المربع قائمة ومتساوية، بينما وفي المقابل لا يمتلك المعين أية زوايا قائمة، كما أن فيه فقط كل زاويتين متقابلتين متساويتان، وأقطار المربع متساوية في الطول، بينما لا تتساوى أقطار المعين في طولها، ويمكن القول في النهاية إن كل مربع هو معين، إلا أن ليس كل معين هو مربع.[٧][٨]
يمكن حساب مساحة المربع من خلال عِدّة طُرق، وهي:
لمزيد من المعلومات والأمثلة حول مساحة المربع يمكنك قراءة المقال الآتي: ما هي مساحة المربع.
يُمكن تعريف محيط المربع على أنه المسافة المحيطة به، ويتم حسابه ببساطة عن طريق اتباع إحدى الطرق الآتية:
لمزيد من المعلومات والأمثلة حول محيط المربع يمكنك قراءة المقالات الآتية: قانون محيط المربع، قانون محيط المربع ومساحته.
يُمكن رسم مُربع باستخدام أربع خطوط مُستقيمة مُتساوية في الطول، وربطها مع بعضها البعض بحيث يَمَس كل ضلع نهاية الضلع الآخر، مع الحرص على أن تكون جميع الزوايا الداخلية الأربع قائمة، ولرسم المُربع على ورقة يجب إحضار مَسطرة، وقلم، وفرجار، وورقة ثمَّ اتِّباع الخُطوات الآتية:[١٤]